Undirected edge inference -- temporal filtering

For reference, here is the impulse response of calcium indicators today, taken from the article on GCaMP6:

Time constants are rather high, almost 1 s for the GCaMP6 variants.

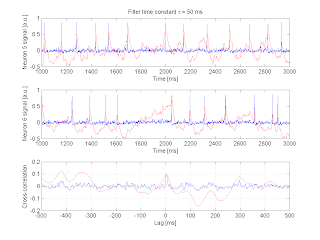
I implemented a basic filtering system, where the impulse response is a simple exponential function characterized with a time constant $\tau$. Here are some representative traces and the filtered output, as well as how the filtering operation modifies the cross-correlation. (The neuron pair shown below are synaptically connected):

It can already be surmised that the temporal filtering will degrade our ability to detect significant correlations. Some thoughts that arise:

• First, it may be the case that the filtering result will depend on the width of the action potential. While the Izhikevich model with the current parameter set produces spikes with reasonable widths, it still may be the case that the widths are dependent on the numerical integration step size.
• Secondly, I wonder if there is a simple closed form formula for determining the resulting cross-correlation when the time series has been temporally filtered. (This seems very plausible.) On the other hand, I'm learning about the limits of cross-correlation for the current task... closed-form formulas for other measures will be harder to obtain.
• Yes, there should be a simple formula here -- will verify soon.
• Thirdly, it appears that we have to "retrain" a $p$-score classifier following temporal filtering.

I now suspect that the "inferrability" of the undirected network will be sharply degraded by the temporal filter. It suggests one line of investigation: is there a mechanism that may allow us to recover the network (e.g. multiple trials, etc.) despite the temporally degraded signals?

I resynthesized the CDF of cross correlations given temporal filtering of $\tau = 5$ ms. It can be seen that the distribution is different from that without the temporal filtering: